It is Time to Start Justifying Sample Sizes in Prediction Model Studies

A fundamental property of all research studies is the sample size of the dataset being analysed; that is, the number of participants included in the study/ dataset. Studies developing clinical prediction models (CPMs) are no exception, but in a recent paper my co-authors and I find that sample sizes are rarely justified in CPM development studies.

Overview

Clinical prediction models (CPMs) are mathematical models/ algorithms that take a set of characteristics/information about an individual and their health (e.g. their age, their sex, their weight etc.) as inputs, and output the risk of a certain event (e.g. development of cardiovascular disease).

There are huge numbers of CPMs developed on a regular basis, across a range of medical areas, each intending to aid clinical processes in some way, e.g. to guide decision-making. Given their potential uses, it is vital that the ways in which CPMs are developed is robust and methodologically sound.

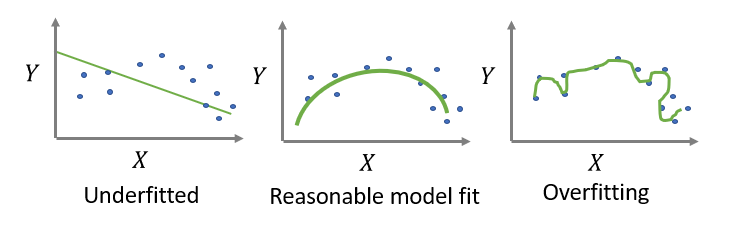
Here, a crucial aspect is the sample size available to develop the model. In other words, studies need sufficient numbers of patients/ observations within the data to develop a robust model. Too low a sample size will likely lead to a phenomenon called “overfitting”, where the model detects too many of the particular subtleties/ nuances within the development dataset, which results in poor predictions in new observations. That is, overfitting means the CPM will not work very well when making predictions in new patients.

Overfitting Illustration

So how large does a dataset need to be for developing a CPM? Well, until very recently, studies generally used something called events per predictor parameter (EPP). EPP is calculated by taking the number of outcomes and dividing by the number of variables/ predictors that one is considering including in the CPM. A rule-of-thumb was that to develop a CPM, the dataset needed to be large enough such that the EPP was greater than 10.

Unfortunately, this is overly simplistic and does not guarantee that a particular dataset has sufficient sample size to develop the CPM.

As such, there has recently been publication of formal sample size criteria (see here, for example; Riley et al. 2019a, Riley et al. 2019b, Riley et al. 2020) that researchers can use to determine the required sample size. These criteria are more specific to the particular CPM and clinical context under investigation, and should therefore be favoured over the EPP rule-of-thumb.

In the paper, my co-authors and I aimed to search the literature and explore how many CPMs that have previously been developed meet these criteria. Given the amount of CPMs developed across medical areas, we opted to restrict ourselves to prostate cancer as an exemplar.

What did we find?

Through our search of the literature, we found 211 CPMs in prostate cancer. Full details of the search and the included studies can be found here. Our main finding was that very few of the included studies justified the sample size that was used to develop the CPM, and those that did mainly used EPP. We also found that very few CPMs (only 48% of included CPMs) were developed on sample sizes that met formal requirements, while many of the CPMs (68% of included CPMs) met the classic EPP>10 rule-of-thumb.

To some extent this is hardly surprising: the formal criteria were published after many of the CPMs included in our study, meaning that studies published in the past cannot be expected to meet recent criteria. Indeed, our paper is not intended to point blame, but rather highlight that this is an outstanding issue in prediction modelling research. The important point is that the classic use of EPP>10 is not necessarily sufficient to ensure studies developing CPMs have sufficient sample size. In most cases, the sample size based on the formal criteria was much higher than needed to meet the EPP>10 rule-of-thumb.

Therefore, it is important that all future studies aiming to develop a CPM carefully justify the sample size that was used, ideally by using the formal criteria. If studies meet the formal sample size criteria, then this gives increased confidence that the risk of overfitting is lower, and is one step (of several steps) in ensuring that the model is robust. Our findings also support previous research in showing that the use of rules-of-thumb around EPP are not sufficient for CPM sample size justification (van Smeden et al. 2016).

To summarise

It is time to start justifying sample sizes when developing a CPM and explicitly describing this within publications aiming to develop CPMs. This, afterall, is recommended within CPM reporting guidelines (TRIPOD; Moons et al. 2015). With the recent publication of formal sample size criteria (Riley et al. 2019a, Riley et al. 2019b, Riley et al. 2020), the research community now has the tools it needs to make such justifications.

Link to the (open access) paper: Collins et al. 2021 here.

References

Collins S.D., Peek N., Riley R.D., Martin G.P. Sample sizes of prediction model studies in prostate cancer were rarely justified and often insufficient. Journal of Clinical Epidemiology, 2021; 133: 53 - 60

Moons KG, Altman DG, Reitsma JB, Ioannidis JP, Macaskill P, Steyerberg EW, et al. Transparent reporting of a multivariable prediction model for Individual Prognosis or Diagnosis (TRIPOD): explanation and elaboration. Ann Intern Med 2015;162:W1e73.

Riley R.D., Snell K.I.E., Ensor J., Burke D.L., Harrell Jr., F.E., Moons K.G.M., et al. Minimum sample size for developing a multivariable prediction model: Part I - continuous outcomes. Stat Med. 2019a; 38: 1262-1275

Riley R.D., Ensor J., Snell K.I.E., Harrell F.E., Martin G.P., Reitsma J.B., et al. Calculating the sample size required for developing a clinical prediction model. BMJ. 2020; 368: m441

van Smeden M., de Groot J.A., Moons K.G., Collins G.S., Altman D.G., Eijkemans M.J., et al. No rationale for 1 variable per 10 events criterion for binary logistic regression analysis. BMC Med Res Methodol. 2016; 16: 163